|
This post is part of my ongoing series on statistics in Starcraft 2. Thus far, I've looked at the network structure of professional games, and explained why ELO is not really appropriate for ranking players by skill. Today, I'll be taking a step back and trying to measure how much of a difference skill makes at the pro level.
The ultimate goal of this project is to build a system of ranking players that won't fall prey to some of the issues that plague ELO. Before we get into the details of such a system, though, it's important to ask whether or not such a system exists. If we want to rank players on one dimension, then it would be important for skill to be approximately one-dimensional, otherwise our results might be meaningless.
Basically, I want to be able to say, these are the top 10 players, in some particular order. In order for that to be accurate, we'd want as few upsets as possible. But I also want to be able to take that one step further, and compare players who haven't played each other yet. If you look at the networks from part 1, you will notice that each of the scenes is fairly segregated, which means that we will need to examine a lot of hypothetical matchups to develop a set of rankings.
Underpinning a lot of the structure of ELO and other ranking mechanisms is the idea of transitivity. Suppose we have three players under consideration, let's call them Adelscott, Bomber, and Catz. We ask each of them to play the other two, and record the results. Hypothetically, let's say Adelscott beats Bomber, Bomber beats Catz, and Catz loses to Adelscott. We call this situation transitive, because one of the players beat the other two (Adelscott in this case). This is a really helpful situation for ranking the players, because Adelscott went 2-0, Bomber went 1-1, and Catz went 0-2. Now, let's suppose instead that Catz had beaten Adelscott. This case is considered non-transitive, because each player went 1-1. Non-transitive cases make ranking players considerably more difficult, since we have no objective data to help us break the tie.
In a perfect world, where the player with "more skill" always won, non-transitivity would never occur. In the opposite world, where every game is determined at random, non-transitivity would occur about 25% of the time. This is because, among three players, there are eight different configurations (2 possibilities for each of 3 games, 2^3 =8). If your having trouble believing this, you can do what I did and draw out the eight possibilities:
![[image loading]](http://i.imgur.com/juN3n.jpg)
Triangles 2-7 are transitive, while #1 & #8 are non-transitive.
A natural question to ask is, are we closer to the perfect world, or the random world? I fired up R to take a look at transitivity among the 293 most prolific pro players around the world.
I utilized the amazing igraph package for R to isolate all of the triads (sets of three players who have played at least one game against each other). In total, there are 20,350 triads to examine. Instead of looking at only one game played between each of the triad members, I look at all of their games against each other from the TLPD. I'm also throwing out all the triads in which two players had an equal number of wins and losses against each other, since I'm not sure how to handle that (these cases were a small minority). Additionally, I've isolated those sets of games played within one of the three scenes, and calculated the triad rate for each of those as well.
So what are the results? Here are the rates of non-transitivity, both for the entire international scene and broken down by continent:
Overall: 16.95%
Asia: 20.35%
America: 17.78%
Europe: 17.04%
The obvious news first: We don't live in a perfect world, but it's also not completely random. It's somewhere in the middle. The Asian scene has higher rates of non-transitivity than either America or Europe. This could be because Asian players tend to play more cheesy strategies, but it could also be an indication that there's less of a skill gap between the best players and the worst players in Asia.
The less obvious news: The overall rate of non-transitivity is lower than any of the regions individually. Keep in mind that games played between opponents from different regions are only counted in the "Overall" rate. Therefore, skill is more of a factor when two players from different regions play, compared to two players from the same region. I take this to mean that there are significant differences in the average skill of players from region to region. This method doesn't tell us which regions are "better" on average, but it does tell us that the three regions are not equal.
On the whole though, I'm not sure precisely how much this proves. I'd like to make the simple conclusion that, since all of the rates are above 12.5%, we live in a world where randomness is more important than skill. The problem is that I'm not sure these rates are sufficient evidence of that fact. It could be that skill is multi-dimensional, which would give a high level of non-transitivity even if randomness is not that important. Your thoughts on this subject would be much appreciated.
----------
Unrelated to the above:
Quick followup - In part 2, I attempted to predict the NASL based on ELO rankings. Out of 16 series, ELO correctly predicted the winners of 8 series. In other words, no better than chance.
Also, I've been working on my new algorithm and it's almost done. I've been getting some really good results, and I can't wait to share them with you guys. If all goes well ironing out the last few bugs, I should have a post up this weekend with the Top 100 players in the world.
As always, any thoughts/critiques are welcome. If any of you have experience with statistics, I'd be curious to get your thoughts on the transitivity test. I looked around for papers on the subject, but I'm not sure anyone has really looked at these kinds of tests before.
    
|
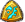
Katowice25012 Posts
wow I missed your other blogs, these are really good. I've wanted to write a piece on why ELO is worthless for SC for years but never could articulate the argument well enough.
Keep up the awesome work! I tried to get some insight into the problem you're having a while back and ended up reading through the MS published papers on how TrueSkill works, but all it did was make me feel like I was even deeper in an endless rabbit hole.
I would really love a better way of objectively ranking players so keep us posted on the results of your algorithm, it has a lot of potential for the larger community as a resource.
|
This could be really interesting. Keep up the good work!
|
This is great. Thanks for all of the work on this as I have been following your write-ups. I cannot wait to see some more results.
|
Wow amazing series of blogs! I can't wait to see your algorithm and its results.
About the non-transitivity: I think that it is going to be a combination of multi-dimensional skill as well as randomness (unfortunately). In SC2, some players may have a playstyle that is particularly strong against a playstyle set, but weak to another. Still randomness is going to be a large factor due to circumstances that we could not account for in an algorithm, such as a player's mental state (micro mistakes, etc) or some luck factor with scouting and positional spawning. Maps and matchup would also play a huge role, and I don't know if you would take this into account.
|
Out of 16 series, ELO correctly predicted the winners of 8 series. In other words, no better than chance.
I read a paper where ELO and other ranking systems were used to predict outcomes of Go matches. ELO was right about 55% of the time, and the other ones were right about 56%. So it is a little better than chance in the long run. Your sample of 16 Bernoulli trials with a ~55% rate of success (assuming ELO is as accurate for SC2 as for Go) could easily land 8 successes, so we can't really conclude it's "no better than chance".
Underpinning a lot of the structure of ELO and other ranking mechanisms is the idea of transitivity. Suppose we have three players under consideration, let's call them Adelscott, Bomber, and Catz. We ask each of them to play the other two, and record the results. Hypothetically, let's say Adelscott beats Bomber, Bomber beats Catz, and Catz loses to Adelscott. We call this situation transitive, because one of the players beat the other two (Adelscott in this case). This is a really helpful situation for ranking the players, because Adelscott went 2-0, Bomber went 1-1, and Catz went 0-2. Now, let's suppose instead that Catz had beaten Adelscott. This case is considered non-transitive, because each player went 1-1. Non-transitive cases make ranking players considerably more difficult, since we have no objective data to help us break the tie.
Note that all three players are of different races, and I don't mean there's one hispanic, one caucasian, and one asian. If, in the second scenario, Adelscott has great PvT and bad PvZ, Bomber has great TvZ and bad TvP, and Catz has great ZvP and bad ZvT, I would say that the results are transitive with regards to matchups. If it's possible to run the analysis with respect to matchups I would love to see the results.
|
Putting statistics in the title guarantees a read and 5-star from me, and I'll bet I aint the only one.
|
I simply play with numbers as a hobby, so my methods are far more primitive in comparison.
Based on my readings, Elo is not a perfect system for StarCraft, but it certainly can be predictive if used properly. For example, while it or other rating system (like yours) will perform poorly for elimination tournaments, it provide certain level of reliability for league-style, round-robin formats. Simple combination of expected values derived only from players' Elos shows approximately 70% hit-rate (NASL group stage, experimentally, with week 3 data), which is non-trivial.
There is no doubt that a better rating system can exist than the traditional Elo (TrueSkill, for one). However, any rating system that tries to distill a player's skill in a single rating will fail to capture certain properties unique to StarCraft. For one, players' skill in each racial matchup varies wildly, and my preliminary tests shows that proper use of that data can add about 5% more accuracy to projections. Another is map-balance. If you also account for these variables in your rating system, I am certain that non-transitivity can be reduced significantly, perhaps around 12% or lower.
|
On July 22 2011 15:43 Cassel_Castle wrote:
Note that all three players are of different races, and I don't mean there's one hispanic, one caucasian, and one asian. If, in the second scenario, Adelscott has great PvT and bad PvZ, Bomber has great TvZ and bad TvP, and Catz has great ZvP and bad ZvT, I would say that the results are transitive with regards to matchups. If it's possible to run the analysis with respect to matchups I would love to see the results.
That's an excellent point. I thought quite awhile about measuring the matchups individually, but I decided against it for two reasons:
1. Identification - Some players in the sample (i.e. DongRaeGu) have played less than 25 games in tournaments. If we broke each player down into three different matchups, we might be identify certain matchup skills based on only a handful of games. Even though we might be taking more aspects of player skill into account, our results might actually be less accurate, due to the fact that we've basically tripled the degrees of freedom.
2. Ranking - My point with this analysis is to try and rank players objectively. If I broke it down by matchup, I'd be ranking player-matchups instead, which would no doubt be interesting, but I'll leave that for another day.
You're absolutely right in that skill could be multi-dimensional, but for the time being I'm going to look at skill on one-dimension. My effort today was to show that skill is not zero-dimensional (aka random). Going forward, I'll try and address these extra possible dimensions by adding them one at a time.
@Primadog:
ELO achieves more accuracy if the disparities in skill between players are wider. Given ELO's faults, I like to think about it as a noisy indicator. If one player is much much better than another, his ELO is likely to be higher as well. However, if the gap in skill is reasonably small, the better player's ELO might be lower than his opponent's rating, due to the noise.
ELO might have done better in the NASL round-robin than in the finals because of the player pool. The round-robin had 50 players, with a wide distribution of skill, whereas the finals had much less variance among its players.
My new algorithm will be capturing a lot of the same information that ELO has, but without the noise. It should do just as well as ELO in the round-robin stages, but outperform ELO in situations like the NASL finals.
|
|
|
|
|
|
![[image loading]](http://i.imgur.com/juN3n.jpg)





